Czym jest modelowanie równań strukturalnych PLS?
Czym jest modelowanie równań strukturalnych? To pytanie zadaje sobie wielu młodych naukowców rozpoczynających swoją karierę badawczą, a nawet i tych starszych którzy nie śledzą postępów z obszarze testowania zaawansowanych modeli statystycznych.
Modele równań strukturalnych (SEM) – Ogólnie
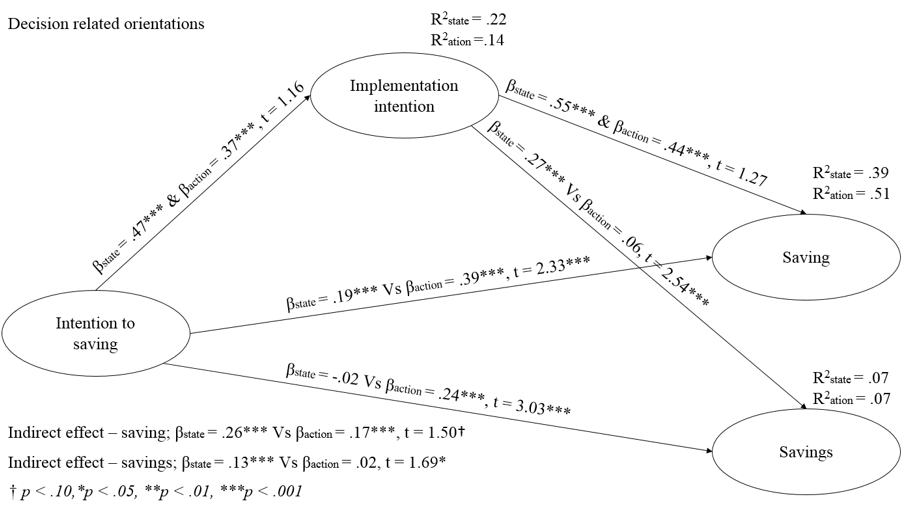
Modele równań strukturalnych (SEM) (Bollen, 1989; Kaplan, 2000) zawierają metodologie statystyczne mające na celu oszacowanie sieci przyczynowych związków definiowanych w zgodzie z testowanym modelem teoretycznym, łączącym dwa lub więcej nieobserwowalnych konceptów, gdzie każdy jest mierzony przez pewną liczbę obserwowalnych wskaźników. Podstawową ideą jest to, że złożone wnętrze systemu sieci relacji może analizowane przy wzięciu pod uwagę przyczynowej sieci powiązań między konceptami ukrytymi, nazywanymi zmiennymi latentnymi. Każda zmienna jest mierzona przez kilka obserwowanych zmiennych zwykle definiowanych jako zmienne manifestujące. Ideę tę można oddać w tym sensie, że Modele Równań strukturalnych reprezentują punkt styku między Analizą Ścieżkową (Tukey, 1964), a Konfirmacyjną Anlizą Czynnikową (Thurstone, 1931). Przykład graficzny takiej reprezentacji przedstawia poniższy rysunek:
* Każda elipsa, to zmienna nieobserwowalna. Każda zmienna nieobserwowalna na rysunku jest odzwierciedlana poprzez obserwowalne jej manifestacje np. pytania w kwestionariuszu badawczym. Powyższe obliczenia wykonano dzieki metodzie SEM-PLS. Do analizy wykorzystano algortym PTH2 kontrolujacy w oszacowaniach błąd pomiaru zmiennych za pomocą współczynnika rzetelności Dijkstra .
Czym jest modelowanie równań strukturalnych PLS?
To czym jest modelowanie równań strukturalnych PLS napiszemy w tym akapicie. Podejście PLS (Partial Least Squares) znane jako PLS Path Modeling (PLS-SEM) zostało zaproponowane jako procedura inna od klasycznego podejścia bazującego na macierzy wariancji-kowariancji CB-SEM. Modelowanie PLS bazuje na metodzie estymacji zmiennych kompozytowych (formatywnych) lub latentnych (reflektywnych) (Tenenhaus, 2008). Jest to podejście w którym główną rolę odgrywania iteracyjny algorytm, który odrębnie wylicza oszacowania związane z modelem pomiarowym modelu strukturalnego, a następnie szacuje wartości ścieżek w modelu strukturalnym. Tak więc, twierdzi się, że PLS-SEM w najlepszym wypadku wyjaśnia wariancję zmiennych nieobserwowalnych przez obserwowalne wskaźniki, a także zmienne poddane jakiejkolwiek regresji w modelu ścieżkowym. To dlatego modelowanie PLS jest rozważane bardziej jako predykcyjne podejście do analizy niż konfirmacyjne. Ma to wiele wad (trudności z porównywaniem modeli), ale sporo zalet (nieparametrycznych charakter anlizy). W przeciwieństwie do klasycznego podejścia bazującego na macierzy wariancji-kowariancji CB-SEM, PLS-SEM nie ma na celu odtworzenia tej macierzy, co stanowi problemy z porówywaniem takich modeli i oceną dopasowania danych.
PLS-SEM jest uważany jako podejście do lekkiego modelowania (soft modeling) w którym nie ma silnych założeń dotyczących kształtu rozkładu danych, wielkości próbki i skali pomiaru testowanych zmiennych. Jest to szczególnie cenna cecha tego podejścia ze względu na to, że wielu obszarach nauki takie założenia trudno spełnić, co najmniej w całości np. w badaniach klinicznych (Kock & Gaskins, 2016; Kock & Hadaya, 2018). Z innej strony sugeruje to brak możliwości wnioskowania parametrycznego, które jest zamienione w PLS na analizę przedziałów ufności i testowanie hipotez poprzez procedury próbkowania bootstrap, jacknife, blindfold lub stabilnego wygładzania wykładniczego (zobacz Stable1, 2, 3 w Kock, 2014). Prowadzi to do mniej ambitnego wnioskowania statystycznego na temat dokładności oszacowań, ale pozwala na maksymalizowanie wyjaśnionej wariancji. W metodzie PLS wiemy, że wspóczynniki są stronnicze ze względu na maksymalizację predykcji, ale w dużej mierze metoda ta zwraca wyniki charakteryzujące się zdecydowaną spójnością.
Podsumowanie
Czym jest modelowanie równań strukturalnych? Wydaje się, że modelowanie metodą PLS jest bardziej podejściem maksymalizującym predykcję (maksymalizuje wyjaśnianie wariancji w modelu pomiarowym i modelu ścieżkowym) niż maksymalizującym dokładność oszacowań. Bez wątpienia modelowanie równń strukturalnych PLS jest metodą statystyczną wartą zainteresowania. Nie tylko ze względu na jej nowość, ale ze względu na jej niskie wymagania dotyczące danych, a co za tym idzie możliwości łatwego i praktycznego zastowowania w badaniach o skomplikowanej naturze pomiarowej i złożoności metodologicznej schematu badawczego.
Zródła:
Bollen, K. A. (1989). Structural equations with latent variables. New York: Wiley.
Kaplan, D. (2000). Structural equation modeling: foundations and extensions. Thousands Oaks, California: Sage.
Kock, N. (2014). Stable P value calculation methods in PLS-SEM. Laredo, TX: ScriptWarp Systems, 1–15. https://doi.org/DOI:10.13140/2.1.2215.3284
Kock, N., & Gaskins, L. (2016). Simpson’s paradox, moderation, and the emergence of quadratic relationships in path models: An information systems illustration. International Journal of Applied Nonlinear Science, 2(3), 200–234. https://doi.org/10.1109/ICUMT.2009.5345351
Kock, N., & Hadaya, P. (2018). Minimum sample size estimation in PLS-SEM : The inverse square root and gamma-exponential methods, 227–261. https://doi.org/10.1111/isj.12131
Vinzi, V. E., Trinchera, L., & Amato, S. (2010). Handbook of Partial Least Squares. https://doi.org/10.1007/978-3-540-32827-8
Tenenhaus, M. (2008). Component-based structural equation modelling. Total Quality Manage- ment & Business Excellence, 19, 871–886
Thurstone, L. L. (1931). The theory ofmultiple factors. Ann Arbor, MI: Edwards Brothers
Tukey, J. W. (1964). Causation, regression and path analysis. In Statistics and mathematics in biology. New York: Hafner