Modelowanie równań strukturalnych (Structural equations modeling – SEM )
Metoda równań strukturalnych, jako najbardziej zaawansowana metoda dowodzenia twierdzeń naukowych, ma swoich zwolenników i krytyków, ponieważ posiada bardzo wiele zalet oraz równie wiele wad. Praca z wykorzystaniem modelowania równań strukturalnych zawsze rozpoczyna się od poznania podstaw teoretycznych elaborowanego zjawiska, tylko na podstawie wytycznych teoretycznych lub różnych ich wariantów można budować model równań strukturalnych. Do jego budowy niezbędne są przewidywania jakie daje teoria lub bardzo silna intuicja. Bez opierania się o te wskazania można zbudować model dopasowany do danych, ale mający niewiele wspólnego z rzeczywistością. Ponad to jeśli będzie on nawet poprawnie skonstruowany i dopasowany, to bez teorii trudne będzie logiczne z niego wnioskowanie i odpowiedzenie na pytanie: Dlaczego zaszły zaobserwowane wyniki?
Modelowanie równań strukturalnych w skrócie
W skrócie, analiza modelowania równań strukturalnych, daje wgląd w badane zjawisko w jego bardzo zaawansowanym wydaniu. Dzięki elastyczności w modelowaniu relacji między zmiennymi możliwe jest uzyskanie dowolnego modelu relacji przyczyn i skutków. Niemniej, niekiedy przy modelowaniu równań strukturalnych trzeba przygotować się na alternatywne scenariusze relacji między zmiennymi. Nie zawsze, teoria przez którą patrzymy na naturę zjawisk daje uchwycić się 1 do 1 w modelu statystycznym. Dlatego warto przygotować odrobinę zmienione struktury przewidywanych korelacji, by móc wybrać model dopasowany lub porównywać modele alternatywne. Dzięki analizie modelowania równań strukturalnych można również badać strukturę kwestionariuszy. W tej odsłonie jest to metoda konfirmacyjna, która potwierdza założenia o strukturze czynnikowej (Konfirmacyjna Analiza Czynnikowa) walidowanego testu oraz pozwala na budowanie alternatywnych jego wersji, by wybrać ten najlepiej dopasowany.
Modelowanie równań strukturalnych
Analiza równań strukturalnych ma na celu analizę kształtu i siły zależności mających charakter funkcji liniowych (lub też nieliniowych) pomiędzy zmierzonymi zjawiskami. Modelowanie może się dążyć do analizy zmiennych formatywnych i reflektywnych (Sarstedt et al., 2016), może uwzględniać moderatory relacji w formie analizy wzrostu zmiennej latentnej (full latent growth analysis) (Kock, 2020) lub porównywać nasilenie ścieżek w podzbiorach wydzielonych inną zmienną (MGA-Multi group Analysis) (Klesel et al., 2019; Rodríguez-Entrena et al., 2016), może testować efekty mediacyjne, a także efekty moderowanej mediacji. Niezwykły postęp dokonuje się w modelowaniu równań strukturalnych, dlatego trudno w krótkim wpisie zintegrować wielość możliwości oferowanych przez tę fascynującą metodę analizy statystycznej.
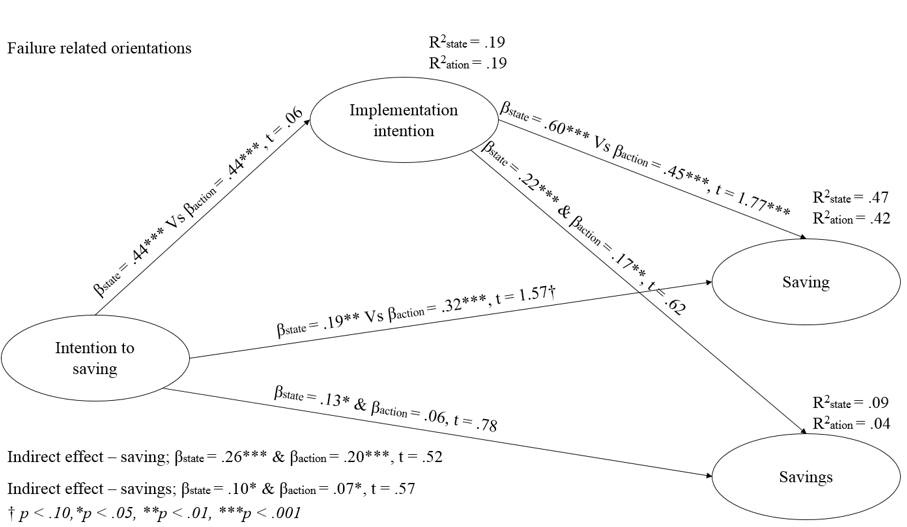
Poniższy rysunek przedstawia model równań strukturalnych wykonanych metodą PLS ze zmienną mediującą, a także zmienną moderującą relacje (State – Action Orientation) (Hryniewicz & Borchet, 2019). Model ten przedstawia niezbyt skomplikowany układ. Niemniej jest przykładem potencjału jaki posiada analiza modelowania równań strukturalnych. Zauważmy, że zmienna niezależna (Intention to saving) jednocześnie wpływa na mediatotr (implementation intention), a te z kolei na oszczędzanie (Saving) i posiadane oszczędności (Savings). Dodatkowo te oszacowania są wyliczone w dwóch porównywanych ze sobą grupach action vs state oriented people.
Poniższy model strukturalny może jeszcze bardziej skomplikować i wprowadzić zmienną czasu, która potencjalnie mogłaby zmieniać zjawisko między czasem t1 i tx. W tedy mielibyśmy do czynienia z modelem wzrostu zmiennej latentnej. Mam nadzieję, że uda mi się zebrać kiedyś takie dane i uzupełnię ten wpis. Więcej na temat poniższego modelu można przeczytać tutaj KLIK
Bibliografia:
(Hryniewicz & Borchet, 2019)Hryniewicz, K. A., & Borchet, J. (2019). Reaching goals through different means: will and cognition in the action of people with low and high action control. Current Issues in Personality Psychology, 7(4). https://doi.org/10.5114/cipp.2019.88298
Klesel, M., Schuberth, F., Henseler, J., & Niehaves, B. (2019). A test for multigroup comparison using partial least squares path modeling. Internet Research, 29(3), 464–477. https://doi.org/10.1108/IntR-11-2017-0418
Kock, N. (2020). Full latent growth and its use in PLS-SEM: Testing moderating relationships. Data Analysis Perspectives Journal, 1(1), 1–5.
Rodríguez-Entrena, M., Schuberth, F., & Gelhard, C. (2016). Assessing statistical differences between parameters estimates in Partial Least Squares path modeling. Quality and Quantity, August, 1–13. https://doi.org/10.1007/s11135-016-0400-8
Sarstedt, M., Hair, J. F., Ringle, C. M., Thiele, K. O., & Gudergan, S. P. (2016). Estimation issues with PLS and CBSEM: Where the bias lies! Journal of Business Research, 69(10), 3998–4010. https://doi.org/10.1016/j.jbusres.2016.06.007