LINEAR MIXED MODELS – Liniowe modele mieszane
Ten artykuł został napisany w celu:
- przedstawienia sytuacji badawczych w jakich LME (Linear Mixed Model / Liniowy model mieszany) powinien być używany
- jakie są zalety korzystania z tej metody
- jak można interpretować wyniki uzyskane tą metodą.
LINEAR MIXED MODELS – Liniowe modele mieszane – Dla lepszego zrozumienia modeli mieszanych posłużymy się danymi z badania Winter and Grawunder (2012), które są udostępnione do użytku w sieci. W badaniu tym modelowano wpływ formalności sytuacji w jakiej znalazł się badany (zmienna dwupoziomowa: prośba formalna vs prośba nieformalna) oraz płci badanych na wysokość tonu głosu. Można więc zapisać tworzony model jako:
Wysokość głosu = formalność sytuacji + płeć + błąd pomiaru
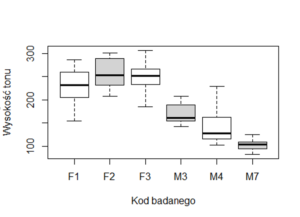
W badaniu tym kilkakrotnie dokonywano pomiaru tego samego badanego w tych samej sytuacji (tzn każdy badany udzielał kilku odpowiedzi w sytuacji formalnej i kilku odpowiedzi w sytuacji nieformalnej, choć sytuacje te były zawsze opisywane w różny sposób). W związku z powyższym te odpowiedzi, które pochodziły od tego samego badanego, były w pewnym stopniu powiązane między sobą. Ludzie różnią się zarówno płcią, wyjściową (normalną dla siebie) wysokością tonu jak i plastycznością swojego zachowania w obliczu różnych sytuacji. Tym samym odpowiedzi udzielone przez jednego badanego były bardziej podobne do siebie niż do odpowiedzi udzielonych przez innego badanego. W celu lepszego zrozumienia tego zjawiska zapoznajmy się z grafiką nr 1 prezentującą rozkład wysokości tonu w obrębie badanej grupy.
Grafika 1. Rozkład wysokości tony w badanej grupie.
Na pierwszy rzut oka widać, że wszystkie kobiety (badani, których kod zaczyna się od litery F) charakteryzowały się wyższymi średnimi wysokościami tonu od badanych mężczyzn. Dodatkowo widać, że niektórzy badani charakteryzowali się mały dysproporcjami w prezentowanych wysokościach tonu (wykres skrzynkowy badanego M7 jest najbardziej spłaszczony co sugeruje małą wariancję tonu jego głosu, zaś np. badana F1 charakteryzowała się już wysoką zmiennością tonu).
LINEAR MIXED MODELS – Liniowe modele mieszane. Podsumowując jeżeli w badaniu pomiary w obrębie wybranych skupisk są ze sobą powiązane (jak na przykład kilka pomiarów wysokości tonu u tego samego badanego) mamy do czynienia ze współzależnością pomiarów a więc nie możemy użyć klasycznej ANOVA dla pomiarów międzygrupowych czy analizy regresji, wymagających spełnienia założenia o niezależności.
Sposobem na rozwiązanie problemu występowania zależności w danych jest dołożenie do naszego wcześniej prezentowanego modelu dodatkowego elementu tj. losowego efektu dla badanego. Założymy tym samym, że każdy badany może charakteryzować się różną średnią wysokością tonu.
Wzór na nasz model wygląda teraz tak:
Wysokość głosu = formalność sytuacji + płeć + (1|badany) + błąd pomiaru
Gdzie (1|badany) oznacza, że każdy badany może się charakteryzować własnym średnim poziomem tonu.
Przejdźmy od razu do wyników jakie otrzymamy po uruchomieniu naszej analizy modelu mieszanego.
Pierwsze na co warto zwrócić uwagę co wydruk z efektami losowymi. W tabeli widać, że zmienność związana z różnymi średnimi poziomami badanych wynosiła 19,58 odchyleń standardowych. Ta wartość sama w sobie jest trudna do interpretacji, natomiast nabiera sensu gdy spojrzymy na wartość nie wyjaśnionej w naszym modelu wariancji (residuals). Nie wyjaśniona wariancja wyniosła 28,98 odchylenia standardowego. Dzięki temu, że w naszym modelu badawczych dokonaliśmy kilkukrotnego pomiaru badanych a następnie wyizolowaliśmy wariancję związaną ze zmienności odpowiedzi wewnątrz poszczególnych badanych, pozbyliśmy się 40% wariancji błędu, która w przeciwnym wypadku zaniżała by trafność naszego modelu.
Tabela
Zestawienie wartości efektów losowych.
| Efekty losowe | ||
| Groups | Wariancja | Odchylenie standardowe |
| Badani | 383.3 | 19.58 |
| Residuals | 839.8 | 28.98 |
Oszacowania efektów stałych interpretuje się tak samo jak w przypadku regresji liniowej. W sytuacji formalnej badani charakteryzowali się istotnie niższy tonem głosu o 19,42 Hz niż w przypadku sytuacji nieformalnej, oraz mężczyźni charakteryzowali się istotnie niższym tonem od kobiet o 108,21 Hz.
Tabela
Zestawienie wartości efektów stałych.
| Efekty stałe: | ||||
| Oszacowanie | SE | t | p | |
| (Stała) | 256,69 | 12,57 | 20,43 | <0,001 |
| Formalność sytuacji (Formalna) | -19,42 | 6,37 | -3,05 | <0,001 |
| Płeć (Mężczyźni) | -108,21 | 17,21 | -6,29 | <0,001 |
Dodatkowo możemy się zapoznać wartościami różnych poziomów wysokości tonu każdego z badanych. Widać, po wartościach z tabeli, iż faktycznie każdy badani faktycznie różnili się między sobą w wysokością tonu, stąd kontrolowanie tej zmiennej jest jak najbardziej słuszne.
Tabela
Zestawienie różnych średnich wartości tonu (Stała) dla wszystkich 6-ciu badanych.
| Stała | Formalność sytuacji (Formalna) | Płeć (Mężczyźni) | |
| F1 | 243,77 | -19,42 | -108,21 |
| F2 | 266,38 | -19,42 | -108,21 |
| F3 | 259,94 | -19,42 | -108,21 |
| M3 | 282,81 | -19,42 | -108,21 |
| M4 | 262,22 | -19,42 | -108,21 |
| M7 | 225,05 | -19,42 | -108,21 |
LINEAR MIXED MODELS – Liniowe modele mieszane – Modele mieszane pozwalają nam na nakładanie na modeli dodatkowych założeń
np. to, że formalność sytuacji w różny sposób wpływa na różnych badanych (możemy wtedy wprowadzić do modelu random slopes, które umożliwią dodatkowe odciążenie modelu o zmienność wynikającą z losowych różnic między badanymi pod kątem tego w jaki sposób reagują oni na rodzaj sytuacji).
Podsumowując, linear mixed models (mieszane modele liniowe) umożliwiają na weryfikacji modeli pochodzących z badań, w których zakładać można występowanie współzależności między losowymi zmierzonymi czynnikami, np.:
- w badaniu w których zbadano wpływ różnych czynników chorobywch na pacjenta, pacjenci którzy byli diagnozowani/leczeni przez tych samych lekarzy będą charakteryzowali się współzależnością (lekarze różnią się zdolnościami, specjalizacjami co wpływa na efekty ich pracy)
- w badaniu w których porównywano tolerancję dzieci w klasach 1-3 szkoły podstawowej na obecność dzieci z obcych kultur w ich klasach, dzieci pochodzące z tej samej klasy (posiadającego tego samego wychowawcę mającego wpływ na sytuacje w klasie) będą charakteryzowały się współzależnością wyników
- w badaniu w którym zadaniem badanych było przypisanie ich zdaniem najbardziej pasującego głosu (męskiego bądź żeńskiego) do 10 poszczególnych wyrazów (5-ciu o rodzaju męskim oraz 5-ciu o rodzaju żeńskim), odpowiedzi w obrębie każdego pojedydynczego badanego będą wzajemnie powiązane jak i odpowiedzi w obrębie każdego pojedynczego wyrazu będą również powiązane. Jeden badany może mieć większe upowanie w głosie damskim niż męskim, jak i pewne słowa mogą większym stopniu od innych skłaniać badanych do przypisania im takiego a nie innego głosu.
By uwzględnić obecność tych współzależności w modelu, konieczne będzie użycie analizy mix model.
Winter, B. (2013). Linear models and linear mixed effects models in R with linguistic applications. arXiv:1308.5499.