Szkolenie z modelowania wielopoziomowego w R
Poniżej przedstawiamy jedno ze szkoleń statystycznych które przygotowaliśmy dla pracowników naukowych uniwersytetu ***. Kod jest zapisany w R Markdawn.
—
title: „*Szkolenie z modelowania wielopoziomowego w R*”
author: „mgr Konrad Hryniewicz – Metodolog.pl”
date: „`r format(Sys.time(), ‚%d %B, %Y’)`”
output:
rmarkdown::html_document:
theme: cerulean
toc: true
toc_float: true
—
**Rozwiązanie dostarczone przez Metodolog.pl**
*spec. ds. Analiz Statystycznych, Metodologii Badań oraz języka R*
**Przydatne strony o R:**
https://www.r-bloggers.com – Nowosci w R i ciekawe wpisy
https://www.r-graph-gallery.com – Galerie wizualizacji danych
https://rpubs.com/ – Ciekawe opracowania problemów i liczne tutoriale
https://www.tidyverse.org/ – Stajnia pakietów R Studio
=
https://cran.r-project.org/ – Podstawowy serwer R
https://cran.r-project.org/web/packages/cSEM/vignettes/cSEM.html – ostatnio zostal tam dodany swietny pakiet do SEM-PLS przez Floriana Schubertha (powiem szczerze, jest kozacki, niemniej trzeba miec mocnieszego kompa do obliczen na wiekszych probach)
**Szkolenie powstawało razem z **
## **Załadowanie do pamięci niezbędnych bibliotek i zbioru danych ** ##
„`{r}
#install.packages(c(„merTools”,”openxlsx”,”dplyr”,”ggplot2″,”tidyverse”,”Hmisc”,”writexl”,”car”,”kableExtra”,”lme4″,”lmerTest”,”jtools”,”merTools”,”sjPlot”)) # instalcja potrzebnych bibliotek
library(„openxlsx”)
library(„dplyr”)
library(„ggplot2”)
library(„tidyverse”)
library(„Hmisc”)
library(„writexl”)
library(„car”)
library(„kableExtra”)
library(„lme4”) # MLM
library(„lmerTest”) # Statytyki diagnostyczne dla MLM
library(„jtools”) # Wyswietlanie eleganckich wydrukow dla modeli regresyjnych w tym MLM
library(„merTools”)
library(„sjPlot”) # Wyswietlanie eleganckich tabel dla modeli regresyjnych w tym MLM
setwd(„…”) #funkcja ustaljaca folder roboczy ze wszystkimi plikami
mydata = openxlsx::read.xlsx(„sen.xlsx”) #funkcja otwierająca plik xlsx z dysku
write.xlsx(mydata, „nowe_dane.xlsx”) #funkcja zapisujaca ramki danych w formacie xlsx
options(scipen = 160) #nikt nie lubi notacji naukowych wiec chcemy wiedzieć w wynikach dużo miejsc po przecinku
set.seed(12345678) #ustalamy ziarno pseudolosowania by wystandaryzowac wyniki analiz
colnames(mydata) # patrzymy jakie mamy nagłówki kolumn
„`
## **Wstęp – Jakie są założenia OLSM i dlaczego są one bardzo często trudne do utrzymania w praktyce badawczej? ** ##
1. Model klasycznej liniowej analizy regresji zakłada (a także większość modeli statystycznych), ze wyniki obserwacji są od siebie niezależne np. mój wzrost nie zależy od Twojego wzrostu.
2. Nachylenia linii regresji np. dotyczące zależności miedzy waga a wzrostem są podobne w podgrupach zmiennej grupującej np. płci, grup zawodowych itp.
3. Zjawisko analizowane na ogólniejszym poziomie może być pewnym „złudzeniem”, czyli tzw. Paradoksem Simpsona mówiące o tym, że zjawiska rozpatrywane fragmentarycznie różnią się od zjawiska rozpatrywanego ogólniej.
ad1. W praktyce badawczej te założenia są często ciężkie do spełnienia np. moja ocena z matematyki może być zależna od ocen mojego kolegi/koleżanki z ławki np. dlatego, że ma ojca który poświęca mu/jej dużo czasu na wspólne uczenie się i ta osoba powiela ten schemat wobec mnie 🙂
ad2. Zależność między potencjałem kulturowym nauczyciela może wiązać się z ocenami dzieci z historii różnie w różnych klasach danej szkoły. W jednej klasie może wpływać silniej, a w drugiej słabiej, ale nadal pozytywnie. W trzeciej natomiast, może wpływać, z jakichś względów oczywiście, bardzo silnie, a w czwartej bardzo słabo, dlaczego? Nie wiadomo, ale wiadomo, ze źródłem tej zmienności może być po prostu nauczyciel historii posiadający jakiś konkretny losowy mix cech.
ad3. To trzeba zobaczyć na własne oczy.
## **Jak możemy modelować zjawiska dzięki modelowaniu wielopoziomowemu?** ##
**Zwykła analiza regresji**
**Indywidualne różnice pod względem zmiennej zależnej (losowe intercepty/ ang. random intercepts)**
Każda grupa/obserwacja ma swoje oszacowanie średniego poziomu mierzonej cechy.
Model ten nazywa się modelem zerowym w którym obserwuje się czy są losowe różnice miedzy grupami/obserwacjami.
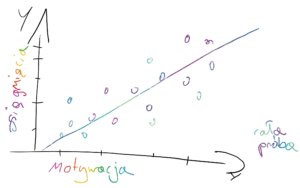
**Losowe różnice pod względem zmiennej zależnej (losowe intercepty/ ang. random intercepts), ale stale linie regresji (ang. fixed slopes)**
Każda grupa/obserwacja ma swoje oszacowanie średniego poziomu mierzonej cechy, ale wpływ zmiennej niezależnej na badane zjawisko jest podobny we wszystkich grupach/obserwacjach.
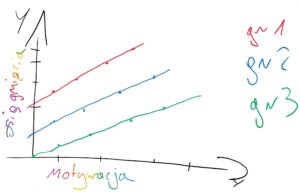
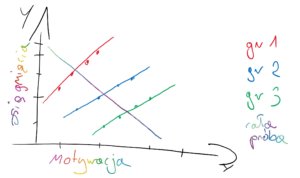
**Brak losowych różnic względem zmiennej zależnej (stale intercepty/ ang. fixed intercepts) oraz zachodzące różnice pod względem nachylenia linii regresji (ang. random slopes)**
Każda grupa/obserwacja ma to samo oszacowanie średniego poziomu mierzonej cechy, ale wpływ zmiennej niezależnej na badane zjawisko jest losowo inny we wszystkich grupach/obserwacjach.
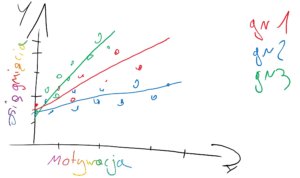
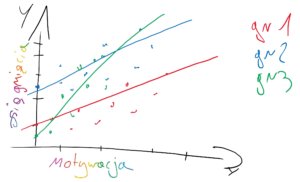
**Losowe różnice względem zmiennej zależnej (losowe intercepty/ ang. random intercepts) oraz różnice pod względem nachylenia linii regresji (ang. random slopes)**
Każda grupa/obserwacja ma rożne oszacowania średniego poziomu mierzonej cechy, ale wpływ zmiennej niezależnej na badane zjawisko jest losowo inny we wszystkich grupach/obserwacjach.
## **Dlaczego efekty mieszane?** ##
Dlatego, że można mieszać w tych modelach elementy random (intercepts i slopes) i fixed (również intercepts i slopes).
## **Opis zbioru danych na jakim będziemy ćwiczyć** ##
Baza danych zawiera informacje o tym jak deprywacja snu przez 10 dni wpływa u różnych ludzi na poziom szybkości reagowania na bodziec wizualny. Domniemuje się, ze im szybszy czas reakcji tym szybciej zachodzą procesy psychiczne w mózgu.
Układ jest bardzo prosty. Poszczególne pomiary dzienne czasu reakcji są zagnieżdżone w osobach. Dzień jest zmienną 1 poziomu (niższy poziom), a osoba jest zmienną 2 poziomu (wyższy poziom). Czas reakcji na bodziec to wartości zmiennej zależnej (wyjaśnianej) powtarzane przez 10 dni u wszystkich osób. Im wyższy czas reakcji, tym wolniejszy czas reakcji na bodziec co jest równoważnie z wolniejszym funkcjonowaniem mózgu i procesów umysłowych.
Na razie nie mamy zmiennych które bardziej określają poziom 1 i 2 analizy. Przez co, nie możemy wykonać interakcji między poziomami, ale do tego typu oszacowań przejdziemy pod koniec. Na razie zaczniemy od podstawowych kwestii związanych z modelowaniem efektów stałych, losowych i mieszanych, a także podstawowa terminologia i statystykami tych modeli.
Podsumowując:
Reakcja = czas reakcji na bodziec (zmienna zależna)
Dni = dzień pomiaru (poziom 1)
Id_Osoby = Id poszczególnych badanych (poziom 2)
*Jak rozpoznać hierarchie w danych?*
– cechy niższego poziomu nie mogą wpływać na cechy wyższego poziomu (uczniowie na nauczyciela lub dzień pomiaru na zachowanie człowieka)
– mamy do czynienia z powtarzanym pomiarem tego samego obiektu (układ wewnątrzobiektowy)
## **Jak wygląda zbiór danych do modelowania wielopoziomowego?** ##
„`{r}
print.data.frame(mydata) #funkcja print.data.frame() pokazuje w konsoli R zbiór danych
„`
## **Model regresji liniowej jedna stała (fixed intercept) i jeden slope (fixed slope)** ##
„`{r}
reg_linear = lm(Reakcja ~ Dni , data = mydata) #Zwykla analiza regresji. Predyktorem jest czas liczony w dniach, a zależną jest szybkość wykonania zadania
jtools::summ(reg_linear) #Podsumowanie modelu regresji
„`
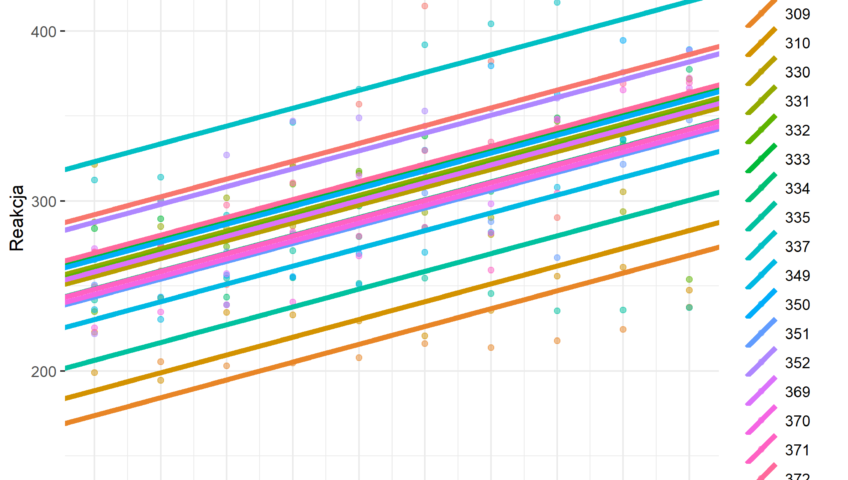
**Rysunek nr 1**
*Wizualizacja zwyklej regresji liniowej z jednym predyktorem (fixed intercept) i jeden slope (fixed slope)*
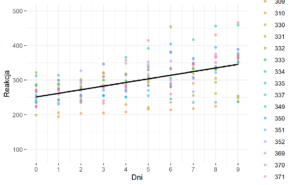
„`{r}
ggplot(data = mydata, mapping = aes(x = Dni, y = Reakcja)) + #definiowanie zbioru danych i zmiennych na wykrescie
geom_point(na.rm = T, aes(col = ID_Osoby), alpha = 0.5) + #pokazanie kolorowych punktów na wykresie rozrzutu względem zmiennej ID_osoby
geom_smooth(method = „lm”, na.rm = T, col = „black”, se = F) + #wykorzystanie funkcji liniowej do wykreślenia linii dopasowania
scale_y_continuous(limits = c(80, 500)) + #skalowanie osi y
scale_x_continuous(breaks = seq(1:10) – 1) + # skalowanie osi x
theme(legend.position = „right”)+theme_bw() + theme(panel.border = element_blank()) #ustawienia szablonu wykresu, pozycji legendy i tła
wykres1 = ggplot(data = mydata, mapping = aes(x = Dni, y = Reakcja)) + #definiowanie zbioru danych i zmiennych na wykrescie
geom_point(na.rm = T, aes(col = ID_Osoby), alpha = 0.5) + #pokazanie kolorowych punktów na wykresie rozrzutu względem zmiennej ID_osoby
geom_smooth(method = „lm”, na.rm = T, col = „black”, se = F) + #wykorzystanie funkcji liniowej do wykreślenia linii dopasowania
scale_y_continuous(limits = c(80, 500)) + #skalowanie osi y
scale_x_continuous(breaks = seq(1:10) – 1) + # skalowanie osi x
theme(legend.position = „right”)+theme_bw() + theme(panel.border = element_blank()) #ustawienia szablonu wykresu, pozycji legendy i tła
ggplot2::ggsave(wykres1, filename = „moj wykres zwykly lm.png”, device = „png”, limitsize = F) #eksport wykresu
„`
## **Model 0 – Testowanie zróżnicowania modelu tylko ze zmienną zależną (wskazując na losowe intercepty dla ludzi/grupy) ** ##
„`{r}
M00 = lme4::lmer(Reakcja ~ 1 + (1|ID_Osoby), data = mydata, REML = F)
model0 = jtools::summ(M00) # Podsumowanie modelu zerowego (bez predyktorow), czyli weryfikacja tego czy nasze osoby różnią się ogólnie pod względem cechy reagowania na bodziec
# Model nie zawiera predyktora, czyli póki co źródłem zróżnicowania pomiarów reagowania jest sam człowiek, czyli jakieś źródło wariancji które identyfikujemy w tym modelu.
# (1 | ID_Osoby) = oznacza, ze intercepty dla poszczególnych ludzi są losowe (czyli, ze ludzie po prostu różnią się pod względem czasu reakcji)
model0
M0_intercepty = lmerTest::ranova(M00) #testowanie istotności zróżnicowania losowości interceptów
M0_intercepty
„`
**Rysunek nr 1b**
*Wizualizacja modelu zerowego losowe stale (random intercepts)*
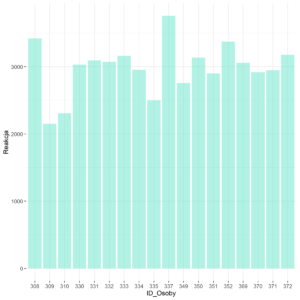
„`{r}
wykres_model_zero = mydata %>% ggplot()+ geom_bar(aes(x=ID_Osoby, y=Reakcja), stat=”identity”, fill=rgb(0.4,0.9,0.8,0.5), alpha=0.5) + theme_bw() + theme(panel.border = element_blank())
ggplot2::ggsave(wykres_model_zero , filename = „wykres_model_zero .png”, device = „png”, limitsize = F) #eksport wykresu
„`
## **Model regresji wielopoziomowej wiele stałych (random intercepts) i jeden slope (fixed slope)** ##
„`{r}
intercepts_model <- lmer(Reakcja ~ Dni + (1 | ID_Osoby), data = mydata, REML = F)
# Regresja wielopoziomowa.
# Predyktorem jest czas liczony w dniach, a zależną jest szybkość wykonania zadania
# (1 | ID_Osoby) = oznacza, ze intercepty dla poszczególnych ludzi są losowe (czyli, ze ludzie po prostu różnią się pod względem czasu reakcji)
jtools::summ(intercepts_model) #Podsumowanie modelu regresji
M0_intercepty = lmerTest::ranova(intercepts_model) #testowanie istotności zróżnicowania małych średnich (interceptów)
M0_intercepty
model_coefs = coef(intercepts_model)$ID_Osoby %>%
dplyr::rename(Intercept = `(Intercept)`, Slope = Dni) %>%
rownames_to_column(„ID_Osoby”)
print.data.frame(model_coefs) #Podsumowanie danych
polaczona_baza_danych_do_wykresu = left_join(mydata, model_coefs, by = „ID_Osoby”) # Połączmy nowe wyliczenia z pierwotną bazą danych
„`
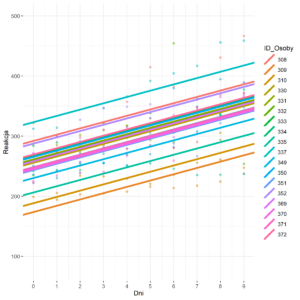
**Rysunek nr 2**
*Wizualizacja zwyklej regresji liniowej z jednym predyktorem z losowymi stałymi (random intercepts) i jednym slopem (fixed slope)*
„`{r}
fized_slopes_random_intercepts = ggplot(data = polaczona_baza_danych_do_wykresu,
mapping = aes(x = Dni,
y = Reakcja,
colour = ID_Osoby)) +
geom_point(na.rm = T, alpha = 0.5) +
geom_abline(aes(intercept = Intercept,
slope = Slope,
colour = ID_Osoby
),size = 1.5) + scale_y_continuous(limits = c(80, 500)) +
scale_x_continuous(breaks = seq(1:10) – 1) +
theme(legend.position = „right”)+theme_bw() + theme(panel.border = element_blank())
ggplot2::ggsave(fized_slopes_random_intercepts , filename = „fized_slopes_random_intercepts.png”, device = „png”, limitsize = F) #eksport wykresu
„`
## **Model regresji wielopoziomowej jedna stałą (fixed intercept) i wieloma slopsami (random slopes)** ##
*Pozdrawiam i zapraszam do modelowania*
„`{r}
slopes_model <- lmer(Reakcja ~ Dni + (0+Dni | ID_Osoby), data = mydata, REML = F)
# Regresja wielopoziomowa
# Predyktorem jest czas liczony w dniach, a zależną jest szybkość wykonania zadania
# (0+Dni | ID_Osoby) = 0 oznacza, ze intercepty dla poszczególnych ludzi są stale (czyli, ze ludzie nie różnią się do siebie pod względem czasu reakcji, ale wpływ dni (zmienna niezależna) na reagowanie (zmienna zależna) jest różny u różnych ludzi)
jtools::summ(slopes_model) #Podsumowanie modelu regresji
M1_slopes = lmerTest::ranova(slopes_model) #testowanie istotności zróżnicowania slopsow u poszczególnych ludzi (pamiętajmy, że intercepty są przyjmują tę samą stałą wartość)
M1_slopes
model_coefs <- coef(slopes_model)$ID_Osoby %>% #Wyliczenie stałego intercepta i losowych slopsów
dplyr::rename(Intercept = `(Intercept)`, Slope = Dni) %>%
rownames_to_column(„ID_Osoby”)
print.data.frame(model_coefs) #Podsumowanie danych
polaczona_baza_danych_do_wykresu = left_join(mydata, model_coefs, by = „ID_Osoby”) # Połączmy nowe wyliczenia z bazą danych
„`
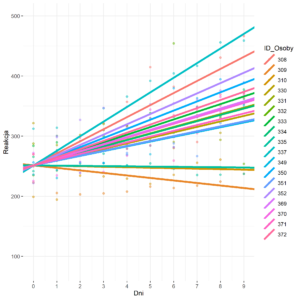
**Rysunek nr 3**
*Wizualizacja zwyklej regresji liniowej z jednym predyktorem z stałą stałą (fixed intercepts) i różnymi slopsami (random slopes)*
 „`{r}
„`{r}
fized_intercepts_random_slopes = ggplot(data = polaczona_baza_danych_do_wykresu,
mapping = aes(x = Dni,
y = Reakcja,
colour = ID_Osoby)) +
geom_point(na.rm = T, alpha = 0.5) +
geom_abline(aes(intercept = Intercept,
slope = Slope,
colour = ID_Osoby
),size = 1.5) + scale_y_continuous(limits = c(80, 500)) +
scale_x_continuous(breaks = seq(1:10) – 1) +
theme(legend.position = „right”)+theme_bw() + theme(panel.border = element_blank())
ggplot2::ggsave(fized_intercepts_random_slopes , filename = „fized_intercepts_random_slopes.png”, device = „png”, limitsize = F)
„`
## **Model regresji wielopoziomowej wiele stałych (random intercepts) i wiele slopsow (random slopes)** ##
„`{r}
intercepts_slopes_model <- lmer(Reakcja ~ Dni + (1+Dni | ID_Osoby), data = mydata, REML = F)
# Regresja wielopoziomowa
# Predyktorem jest czas liczony w dniach, a zależną jest szybkość wykonania zadania
# (1+Dni | ID_Osoby) = 1 oznacza, ze intercepty dla poszczególnych ludzi znów są losowe (czyli, ze ludzie różnią się od siebie pod względem czasu reakcji i tez tego jak upływ czasu wpływa na reagowanie)
jtools::summ(intercepts_slopes_model) #Podsumowanie modelu regresji
M1_slopes = lmerTest::ranova(intercepts_slopes_model) #testowanie istotności zróżnicowania komponentu losowego
M1_slopes
model_coefs <- coef(intercepts_slopes_model)$ID_Osoby %>% #Wyliczenie losowego intercepta i losowego slopsa
dplyr::rename(Intercept = `(Intercept)`, Slope = Dni) %>%
rownames_to_column(„ID_Osoby”)
print.data.frame(model_coefs) #Podsumowanie danych
polaczona_baza_danych_do_wykresu = left_join(mydata, model_coefs, by = „ID_Osoby”) # Połączmy nowe wyliczenia z naszą bazą danych
„`
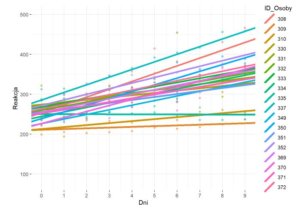
**Rysunek nr 4**
*Wizualizacja zwyklej regresji liniowej z jednym predyktorem z losowymi stałymi (random intercepts) i różnymi slopsami (random slope)*
„`{r}
random_intercepts_random_slopes = ggplot(data = polaczona_baza_danych_do_wykresu,
mapping = aes(x = Dni,
y = Reakcja,
colour = ID_Osoby)) +
geom_point(na.rm = T, alpha = 0.5) +
geom_abline(aes(intercept = Intercept,
slope = Slope,
colour = ID_Osoby
),size = 1.5) + scale_y_continuous(limits = c(80, 500)) +
scale_x_continuous(breaks = seq(1:10) – 1) +
theme(legend.position = „right”)+theme_bw() + theme(panel.border = element_blank())
ggplot2::ggsave(random_intercepts_random_slopes , filename = „random_intercepts_random_slopes.png”, device = „png”, limitsize = F)
„`
## **Porównywanie modeli pod względem dopasowania danych do rozpatrywanych modeli** ##
Niższy wynik AIC, BIC świadczy o lepszym dopasowaniu danych do modelu. Miary te nie maja wartości referencyjnych.
„`{r}
stats::anova(intercepts_slopes_model, slopes_model) #funkcja anova() pozwala na testowanie różnice miedzy modelami pod względem dopasowania danych do modelu
stats::anova(intercepts_slopes_model, intercepts_model)
stats::anova(slopes_model, intercepts_model)
„`
„`{r}
sjPlot::tab_model(M00, intercepts_model, slopes_model,intercepts_slopes_model, show.df = TRUE,show.aic = T, show.se = T ) #Funkcja tab_model() pakietu „sjPlot” elegancko zagnieżdża modele w jednej tabeli. Funkcja ta ma wiele innych fajnych ustawień.
„`